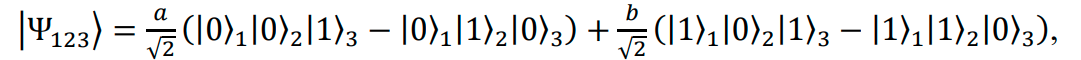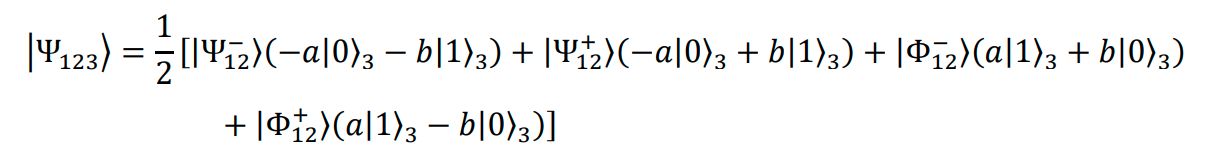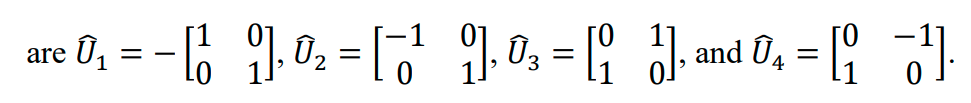Living cells can now be reimagined as programmable “biocomputers,” executing genetic instructions encoded in RNA and DNA to perform therapeutic and diagnostic functions. Researchers at MIT and partner institutions have pioneered languages and compilers—akin to software development tools—that translate high-level circuit descriptions into specific nucleotide sequences. These biocodes enable cells to monitor biomarkers, process logical operations, and trigger precise responses such as insulin secretion or self-destruction of cancerous cells.

High-Level Design: From Logic Diagrams to DNA Sequences​

At the core of this approach lies a software framework called Cello, often dubbed the “programming language for living cells.” Users write programs using a syntax similar to hardware description languages (e.g., Verilog), specifying desired input–output behaviors and logic gates. Cello’s compiler then selects and assembles standardized genetic parts—promoters, ribosome binding sites, terminators—and optimally arranges them into a DNA sequence that implements the logic within Escherichia coli (or other chassis organisms). The result is a plasmid that, when introduced into cells, runs the designed circuit autonomously.

Building on the original Cello, Cello 2.0 expands capabilities with a richer parts library, support for new hosts, formalized design rules, and a graphical user interface. It embraces Verilog 2005 syntax, integrates with repositories like SynBioHub, and uses mathematical models to predict dynamic behavior—streamlining design-build-test cycles in synthetic biology.

Sensor Modules: Detecting Cellular Events with RNA Switches​

Programmable cells require sensors that convert molecular cues into digital-like signals. Researchers leverage toehold switches—engineered RNA structures that remain inactive until a specific trigger RNA opens the switch, allowing translation. MIT’s team introduced eToehold sensors built on internal ribosome entry sites (IRES) that can recognize aberrant mRNAs (e.g., mutated p53) and selectively turn on therapeutic genes only in target cells.

Moreover, CRISPR-based transcriptional regulators can function as programmable logic gates. By designing guide RNAs (gRNAs) that recruit dead Cas9 (dCas9) fused to activator or repressor domains, circuits can activate or repress genes in response to multiple inputs. Data-driven models predict how gRNAs targeting different genomic loci modulate expression, enabling fine control of metabolic and therapeutic pathways.

Logic Cores: RNA- and DNA-Based Gate Architectures​

• Once inputs are sensed, the circuit’s logic core processes them through modular gates:

• RNA logic circuits combine toehold switches and aptamers to implement Boolean functions (AND, OR, NOT) at the mRNA level, ensuring rapid responses.

• Recombinase-based systems employ site-specific recombinases (e.g., Cre, Flp) that invert or excise DNA segments upon detection of triggers, creating permanent memory and enabling multi-step decision trees.

• Protein-level logic integrates transcription factors and synthetic regulators to generate graded or switch-like responses at the transcriptional level.

Introduction: A Quieter Path to Quantum Power​

Amidst the global race for quantum supremacy, dominated by discussions around discrete-variable quantum systems and qubits, a subtler but equally powerful approach is gaining momentum: Continuous Variable Quantum Computing (CVQC). Unlike the binary logic of qubit-based architectures (which rely on two-level systems like spin-up or spin-down), CVQC operates on continuous degrees of freedom—such as the amplitude and phase of electromagnetic fields. This paradigm offers a fundamentally different way to process quantum information.

The Core of CVQC: From Qubits to Quadratures​

In CVQC, quantum information is encoded not in discrete 0s and 1s but in continuous variables, typically associated with the quadratures of light modes—position and momentum-like observables of bosonic fields. These observables are manipulated using Hamiltonian dynamics governed by operators like squeezing, displacement, and beam-splitting, all of which are implementable via quantum optics.

This model leverages Gaussian states and operations, which are relatively easy to generate and control experimentally using optical systems. Furthermore, the measurement techniques such as homodyne and heterodyne detection allow for precise readout of these variables, enabling real-time manipulation of quantum states in continuous domains.

Applications and Advantages​

CVQC finds its strengths in specific quantum tasks:

• 🔐 Quantum Cryptography: Continuous-variable quantum key distribution (CV-QKD) protocols are already operational in some settings, offering high data rates and robust security under realistic noise conditions.

• 🧪 Quantum Simulation: It provides an efficient platform for simulating complex quantum field dynamics and many-body interactions—especially in photonic systems where scalability remains a challenge in qubit-based systems.

• 💡 Quantum Machine Learning & Data Processing: Optical neural networks based on CVQC models offer compelling approaches to analog quantum computing, leveraging high bandwidths of optical systems.

One of the most promising aspects of CVQC is its hardware accessibility. Since it primarily uses photonics, it can operate at room temperature and avoids the cryogenic constraints of many superconducting qubit systems.

Challenges and Theoretical Depth​

Despite its promise, CVQC is not without limitations. One major concern lies in the non-Gaussian operations—crucial for universal quantum computing—which are harder to implement reliably. Moreover, error correction schemes for continuous variables are more complex due to the infinite-dimensional Hilbert space and require innovative code structures such as Gottesman-Kitaev-Preskill (GKP) states.

Nevertheless, advances in optical quantum technologies, integrated photonics, and hybrid systems are slowly bridging these gaps, offering a future where CVQC may complement—or even surpass—qubit-based models in specific applications.

Conclusion: Beyond Qubits, Beyond Noise​

Continuous Variable Quantum Computing presents a less noisy, highly scalable, and theoretically rich framework that challenges the binary lens through which we often view quantum mechanics. By embracing continuous logic, we step into a domain where the boundary between classical wave systems and quantum behavior blurs—unlocking new potential for quantum optics, information theory, and the next generation of computing.

Quantum Teleportation for Control of Dynamical Systems and Autonomy​

• Farbod Khoshnoud​

Electromechanical Engineering Technology Department, College of Engineering, California State Polytechnic University, Pomona, CA 91768, USA. Center for Autonomous Systems and Technologies, Department of Aerospace Engineering, California Institute of Technology 1200 E California Blvd, Pasadena, CA 91106, USA.

• Lucas Lamata​

Atomic, Molecular and Nuclear Physics Department, University of Seville, 41080 Sevilla, Spain.

• Clarence W. de Silva​

Department of Mechanical Engineering, University of British Columbia, Vancouver, BC V6T 1Z4, Canada.

• Marco B. Quadrelli​

Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109, USA.

Abstract​

The application of Quantum Teleportation for control of classical dynamic systems and autonomy is proposed in this paper. Quantum teleportation is an intrinsically quantum phenomenon, and was first introduced by teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels in 1993. In this paper, we consider the possibility of applying this quantum technique to autonomous mobile classical platforms for control and autonomy purposes for the first time in this research. First, a review of how Quantum Entanglement and Quantum Cryptography can be integrated into macroscopic mechanical systems for controls and autonomy applications is presented, as well as how quantum teleportation concepts may be applied to the classical domain. In quantum teleportation, an entangled pair of photons which are correlated in their polarizations are generated and sent to two autonomous platforms, which we call the Alice Robot and the Bob Robot. Alice has been given a quantum system, i.e. a photon, prepared in an unknown state, in addition to receiving an entangled photon. Alice measures the state of her entangled photon and her unknown state jointly and sends the information through a classical channel to Bob. Although Alice’s original unknown state is collapsed in the process of measuring the state of the entangled photon (due to the quantum non-cloning phenomenon), Bob can construct an accurate replica of Alice’s state by applying a unitary operator. This paper, and the previous investigations of the applications of hybrid classical-quantum capabilities in control of dynamical systems, are aimed to promote the adoption of quantum capabilities and its advantages to the classical domain particularly for autonomy and control of autonomous classical systems.

Key Words​

Quantum teleportation, quantum entanglement, quantum cryptography, quantum robotics and autonomy, quantum controls, quantum multibody dynamics.

1. Introduction​

Quantum teleportation is a fundamental quantum concept that allows one to distribute quantum states between distant parties, without measuring or having information about them. In future networks of robots with quantum processing, quantum communication, and quantum sensing capabilities, this quantum primitive, quantum teleportation, might enable a better communication between robots. This will allow one, for example, to transfer the outcome of a quantum processing from one robot to a distant robot, for further quantum processing starting with this quantum state.

Quantum Teleportation by teleporting an unknown quantum state via dual classical and EinsteinPodolsky-Rosen channels was introduced in 1993 [1], which has been demonstrated experimentally [2] and with deterministic approaches (e.g., [3]-[4]). Measurement of the Bell operator and quantum teleportation was introduced in 1995 [5]. Since then, various efforts in development of Quantum Teleportation have been carried out including: Efficient Teleportation Between Remote Single-Atom Quantum Memories [6], Gain tuning for continuous-variable quantum teleportation of discrete-variable states [7], Unconditional Quantum Teleportation [8], Complete quantum teleportation using nuclear magnetic resonance [9], probabilistic resumable quantum teleportation of a two-qubit entangled state [10], Quantum Teleportation Between Discrete and Continuous Encodings of an Optical Qubit [11], Quantum teleportation over the Swisscom telecommunication network [12], and Quantum teleportation-based state transfer of photon polarization into a carbon spin in diamond [13].

The organization of the paper is as follows. A review of Quantum Multibody Dynamics, Controls, Robotics and Autonomy ([14]-[17]) is given. In this review, quantum entanglement (Section 2.1) and quantum cryptography (Section 2.2) are used for hybrid classical-quantum control of classical multi-agent autonomous systems. In Section 2.3, the concept of Quantum Teleportation in conjunction with application to dynamical systems for autonomy is introduced.

2. Quantum multibody dynamics​

Quantum Multibody Dynamics is referred to as the subject of applying quantum physical phenomena (such as quantum entanglement and superposition) integrated with control of a distributed classical dynamical system (such as multiple robots and autonomous systems), and analysing the resulting behaviour of the classical dynamic system when the quantum phenomenon is leveraged for control or communication purposes. Examples include the application of quantum entanglement and quantum cryptography protocols to control of robotic systems presented below, which is then further extended to the application of Quantum Teleportation for control and autonomy purposes in this paper as follows. A review on our proposal for how quantum entanglement and quantum cryptography can be integrated into physical mechanical systems for control and autonomy applications ([14]-[17]) is given in Section 2.1 and Section 2.2.

2.1 Quantum entanglement for dynamic systems​

An experimental setup for quantum entanglement is shown in Figure 1. The proposed procedure of using quantum entangled photons for applications in control of autonomous platforms (Figure 1 to Figure 3), is presented as follows ([14]-[17]), as a hybrid quantum-classical process:

Quantum part:​

• Single photons (pump photons) of 405 nm wavelengths, are generated by a laser diode source.

• Spontaneous parametric down-conversion (SPDC) process is carried out using a nonlinear crystal, beta-barium borate (BBO), to split the 405 nm photon beams into correlated entangled pairs of 810 nm wavelength photons. The entangled photon pairs thus generated that are orthonormal in their polarizations.

• The entangled photons are sent from the BBO crystal to two beamsplitters (BS) that pass the photons with horizontal polarization and reflect the photons with vertical polarization.

• Four Single Photon Counter (SPC) modules are placed as in Figure 1 to Figure 3, where each SPC counts the number of photons reaching them, and keeps track of the corresponding horizontal and polarizations (as they pass or are reflected by the beamsplitter, respectively).

• There are two SPC modules on each autonomous platform. Therefore, each of the autonomous platforms receives an entangled photon as explained above. This is interpreted as entangling the autonomous platforms (i.e., robots are sharing entangled photon pairs) by corresponding entangled photons that are detected by the SPC modules.

• A Coincidence Counter module records the time at which the photons are reaching the SPC modules. If the time that a photon pair reaches two SPCs (on two robots), regardless of the polarization of the photons, is within a small enough time window (e.g., less than 10 ns), then the photon pair are considered as correlated entangled pairs.

Classical part:​

• The horizontal and vertical polarizations that are received by the SPC modules are converted to 0 and 1 digital signals, respectively, to be used for control of the robotic platforms.

• The corresponding digital signals that are obtained from the entangled photon polarizations are sent to digital microcontrollers onboard.

• Desired control tasks, such as motion commands sent to servomotors onboard, are defined correspondingly to the digital signals received.

• The polarizers in between the BBO and the beamsplitters (Figure 1 and Figure 2) is used as controller tools. They provide the capability of controlling the polarization of the photons as they pass through them, which alter the polarization of the entangled photons (e.g., horizontal and vertical polarizations).

Figure 1. An experimental setup for quantum entanglement of autonomous platforms.

Figure 2. Quantum entanglement of autonomous platforms.

Figure 3. Autonomous platforms sharing quantum entangled photon pairs (the Alice Robot and the Bob Robot).

Figure 4. The Alice Robot

2.2 Quantum cryptography for dynamic systems​

The quantum cryptography setup for control of autonomous platforms (e.g., robots) is illustrated in Figure 5. This setup is installed on the same mobile robots in Figure 1 to Figure 4. Only the quantum cryptography system components are shown in Figure 5 (there is no quantum entanglement system component in Figure 5) for clear illustration of the setup. The quantum cryptography technique can be used to encrypt and transfer control commands from the Alice Robot to the Bob Robot (Figure 1 to Figure 5). The quantum cryptography communication technique can be used on its own for control of autonomous systems. In the case of using quantum cryptography in conjunction with quantum entanglement, one technique is to first entangle the robots by the quantum entanglement technique (Section 2.1), and then use the entanglement as a trigger to start the transfer the control commands from the Alice Robot to the Bob Robot.

The Quantum Cryptography process is as follows.

Quantum part:​

• A single photon is sent from the Alice Robot (Figure 4).

• A polarizer placed on the Alice Robot is used to control the polarization of the photon as |−45o⟩,|0o⟩, |45o⟩, and |90o⟩.

• A polarizer placed on the Bob Robot has additional control on the photon polarization with |0o⟩,|45o⟩ orientations.

• After passing through the two polarizers, the photon reaches the beamsplitter which allows the photons with horizontal polarizations to pass, and the photons with vertical polarizations to reflect.

• There is a dedicated sensor for each direction of the photon, which either passes or is reflected by the beamsplitter.

Classical part:​

• The sensor that is dedicated for detecting the horizontally polarized photons sends a digital 0 signal to a digital microcontroller every time that receives a photon. The sensor that receives vertical polarized photons sends digital 1 signal to the microcontroller.

• Desired control commands are defined based on these digital signals for application of autonomy and robotic tasks.

The detailed discussions of the quantum cryptography protocols and the detection of the eavesdropper are presented in references [14]-[17]. Autonomous platforms that are considered in this research (in integrating quantum technologies with mechanical systems) include any stationary or mobile system such as the ground robots in Figure 2 to Figure 4, or aerial systems such as the drones in Figure 7 and Figure 8.

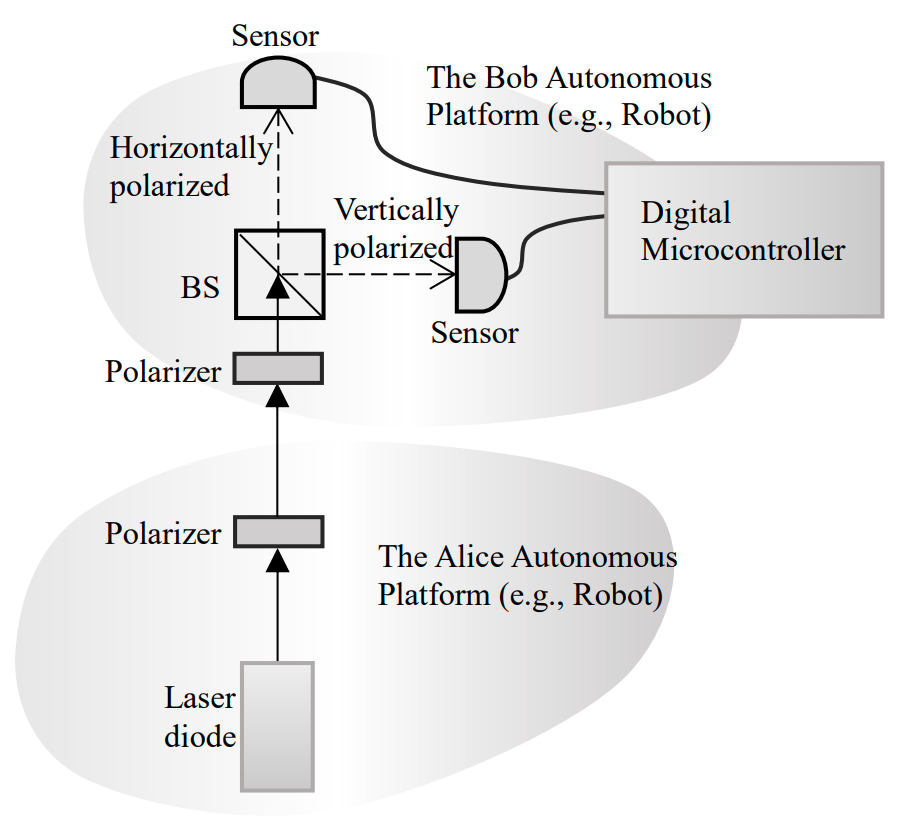
Figure 5. Quantum cryptography.

Figure 6. The Bob Robot.

Figure 7. The Bob Ground Robot and the Alice Drone.

Figure 8. The Alice Drone.

2.3 Quantum teleportation for dynamic systems​

The application of Quantum Teleportation for quantum control of classical dynamic systems and autonomy is proposed here. The Quantum Teleportation technique presented in this section is based on ‘teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen (EPR) channels’ [1]. In a classical system a bit can be copied and transferred (or cloned). By the “No-Cloning Theorem” [18], a quantum state as a quantum bit, or qubit, unlike the classical bit, can not be copied or cloned. Transfer of a qubit from one position (Alice) to another (Bob) is proposed to be carried out by a Quantum Teleportation technique [1]. Quantum Teleportation is applicable to quantum information, quantum cryptography, and quantum control areas. If a qubit is physically (classically) transported, for instance from A to B, the required quantum information can be lost. This is due to the sometimes short coherence times of the quantum states. The Quantum Entanglement phenomenon allows Quantum Teleportation under the assumption that strong correlation between quanta can be maintained.

We propose to apply quantum teleportation of dual classical and Einstein-Podolsky-Rosen (EPR) channels technique to mechanical systems, such as autonomous mobile platforms, for control and autonomy purposes here for the first time. In quantum teleportation, an entangled pair of photons which are correlated in their polarizations are generated and sent to two autonomous platforms, which we call Alice Robot and Bob Robot. Alice has been given a quantum system, i.e. a photon, prepared in an unknown state. Alice also receives one of the entangled photons. Alice measures the state of her entangled photon and sends the information through a classical channel to Bob. Although Alice’s original unknown state is collapsed in the process of measurement, due to quantum non-cloning phenomenon, Bob can construct an accurate replica of Alice’s state by applying a unitary operator.

This paper and the previous investigations of the applications of quantum capabilities in control of dynamical systems are aimed to promote the adoption of unmatched quantum capabilities and advantages in the classical domain particularly for autonomy and control of autonomous systems. In this context, the basic scheme of quantum teleportation is as in Figure 1 and Figure 2. In Quantum Teleportation, the goal is to transfer a quantum state |𝜙1⟩ from the Alice Robot to the Bob Robot. The quantum teleportation process can be notionally described as follows.

• Alice generates the quantum state |𝜙1⟩ to transfer to Bob, where |𝜙1⟩ = 𝑎|0⟩1 + 𝑏|1⟩1 , with |𝑎|2 + |𝑏|2 = 1.

• Quantum entangled states are sent from the BBO (Figure 1 and Figure 2) to Alice and Bob by the SPDC process. Using Bell basis, the basis of a pair of entangled photons (e.g., a two-qubit-system), which are correlated by means of their polarizations, is given by

• Alice and Bob receive the entangled photons.

• Alice makes a complete measurement of the entangled photon (that receives), and the state |𝜙1⟩. Thus, the measurement of the state |𝜙1⟩ and the entangled state |Ψ23− ⟩ can be represented as

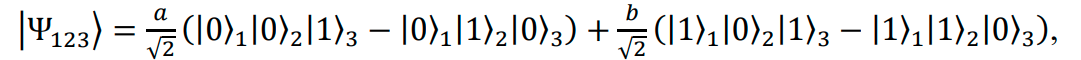
• After Alice’s measurement, Bob's particle (with indices 3) will have been projected into one of the four pure states superposed, with equal possibilities. Bob's particle 3 can be presented by the products of the states in terms of the Bell operator basis as

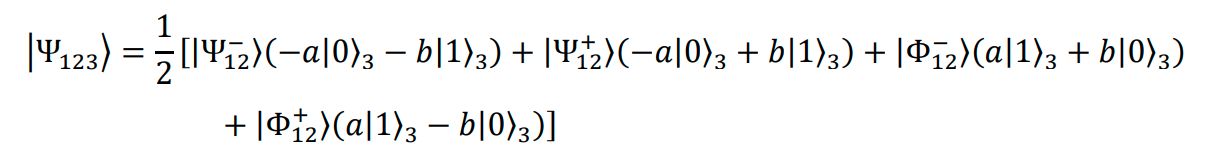
• One of the above Bob’s entangled states (one of the four possibilities) is related to the state, |𝜙1⟩, that Alice is to teleport to Bob. Bob is required to produce a replica of Alice's state.

• Alice's measurement is transmitted as classical information through a classical channel to Bob.

• Bob uses the transmitted information from Alice and applies a set of corresponding unitary transformations on his EPR, according to the Alice’s transmitted state. The unitary transformations

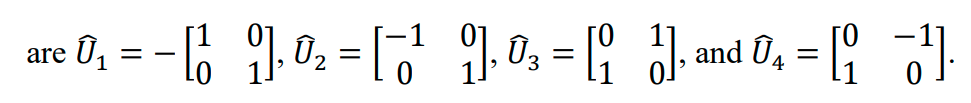
• This transformation brings Bob’s particle to the state of Alice's particle 1 (|𝜙1⟩ ), and the teleportation process is complete.

On the application of quantum teleportation in the context of robotics and autonomy schemes, the Alice Robot teleports a state |𝜙1⟩ to the Bob Robot. Bob converts the polarization information received from Alice into corresponding 0 and 1 digital information, which is then processed by on-board microcontrollers for performing predefined robotic and autonomy tasks.

By accessing quantum computers in future, the on-board classical computation using microcontrollers may be instead realized by quantum processors. In fact, the application of future quantum computers in a network of multi-agent dynamic systems, is only logical if quantum-based techniques such as entanglement and teleportation are employed, rather than any classical wireless communication protocol in the communication network. In a network of autonomous platforms where multiple robotic agents containing quantum processors are communicating with each other, using any classical communication technique may actually defeat the advantages of quantum-enhanced protocols.

Conclusion​

We introduced the integration of quantum mechanical phenomena, such as quantum entanglement, into classical mechanical systems, such as mobile autonomous platforms, as a hybrid classical-quantum system. In particular, the concept of quantum teleportation by teleporting a quantum state via dual classical and Einstein-Podolsky-Rosen channels in the context of the control of dynamical systems and autonomy was proposed. A review of the applications of quantum entanglement and quantum cryptography in developing quantum-enhanced networks of robotic systems was presented. A proposed procedure of how quantum technologies could be brought into the domain of classical mechanical systems by employing quantum entanglement, cryptography and teleportation was described. The research outlined in this paper serves as a first step towards the application of the advantages of quantum techniques in the physical domain of macroscopic dynamic systems. Furthermore, this investigation aims to promote future attempts at exploring the interdisciplinary interface of quantum mechanics and classical system autonomy schemes, by pushing the engineering boundaries beyond any existing classical technique. Using on-board quantum processors, instead of classical microcontrollers, is proposed as one future direction of this research.

Acknowledgement​

Lucas Lamata acknowledges the funding from PGC2018-095113-B-I00, PID2019-104002GB-C21, and PID2019-104002GB-C22 (MCIU/AEI/FEDER, UE). Government sponsorship acknowledged. Dr. Quadrelli’s contribution was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.

References​

[1] C.H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, & W.K. William, Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels, Physical Review Letters, Vol. 70, No. 13, 1993, 1896-1899.

[2] D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter, & A. Zeilinger, Experimental quantum teleportation, Nature 390, 1997, 575-579.

[3] M.D. Barrett, J. Chiaverini, T. Schaetz, J. Britton, W.M. Itano, J.D. Jost, E. Knill, C. Langer, D. Leibfried, R. Ozeri, & D.J. Wineland, Deterministic quantum teleportation of atomic qubits, Nature, Vol. 429, 2004, 737–739.

[4] K.S. Chou, J.Z. Blumoff, C.S. Wang, P.C. Reinhold, C.J. Axline, Y.Y. Gao, L. Frunzio, M.H. Devoret, L. Jiang, and & R.J. Schoelkopf, Deterministic teleportation of a quantum gate between two logical qubits, Nature, Vol. 561, 2018, 368-373.

[5] S.L. Braunstein, & A. Mann, Measurement of the Bell operator and quantum teleportation, Physical Review A, 51, R1727(R), 53, 1995, 630.

[6] C. Nölleke, A. Neuzner, A. Reiserer, C. Hahn, G. Rempe, & S. Ritter, Efficient Teleportation Between Remote Single-Atom Quantum Memories, Physical Review Letters, 110, 2013, 140403.

[7] S. Takeda, T. Mizuta, M. Fuwa, H. Yonezawa, P. van Loock, & A. Furusawa, Gain tuning for continuous-variable quantum teleportation of discrete-variable states, Physical Review A, 88, 2013, 042327.

[8] A. Furusawa, J.L. Sørensen, S.L. Braunstein, C.A. Fuchs, H.J. Kimble, & E.S. Polzik, Unconditional Quantum Teleportation, Science, Vol. 282, Issue 5389, 1998, 706-709.

[9] M.A. Nielsen, E. Knill, & R. Laflamme, Complete quantum teleportation using nuclear magnetic resonance, Letters to Nature, Vol 396, 1998, 52-55.

[10]Z.-Y. Wang, Y.-T. Gou, J.-X. Hou, L.-K. Cao, & X.-H. Wang, Probabilistic Resumable Quantum Teleportation of a Two-Qubit Entangled State, Entropy, 21, 2019, 352; doi:10.3390/e21040352.

[11]A.E. Ulanov, D. Sychev, A.A. Pushkina, I.A. Fedorov, & A.I. Lvovsky, Quantum Teleportation Between Discrete and Continuous Encodings of an Optical Qubit, Physical Review Letters, 118, 2017, 160501. DOI: 10.1103/PhysRevLett.118.160501.

[12]O. Landry, J.A.W. van Houwelingen, A. Beveratos, H. Zbinden, & N. Gisin, Quantum teleportation over the Swisscom telecommunication network, Journal of Optical Society of America B, Vol. 24, No. 2, 2007, 398–403.

[13]K. Tsurumoto, R. Kuroiwa, H. Kano, Y. Sekiguchi, & H. Kosaka, Quantum teleportation-based state transfer of photon polarization into a carbon spin in diamond, Communications Physics, 2:74, 2019. https://doi.org/10.1038/s42005-019-0158-0.

[14]F. Khoshnoud, I.I. Esat, M.B. Quadrelli, D. Robinson, Quantum Cooperative Robotics and Autonomy, Special issue of the Instrumentation Journal, Edited by C.W. de Silva, Vol. 6, No. 3, pp. 93-111, 2019.

[15]F. Khoshnoud, I.I. Esat, S. Javaherian, & B. Bahr, Quantum Entanglement and Cryptography for Automation and Control of Dynamic Systems, Special issue of the Instrumentation Journal, Edited by C.W. de Silva, Vol. 6, No. 4, pp. 109-127, 2019.

[16]F. Khoshnoud, I.I. Esat, C.W. De Silva, M.B. Quadrelli, Quantum Network of Cooperative Unmanned Autonomous Systems, Unmanned Systems, Vol. 07, No. 02, 2019, 137-145.

[17]F. Khoshnoud, D. Robinson, C.W. De Silva, I.I. Esat, R.H.C. Bonser, M.B. Quadrelli, Researchinformed service-learning in Mechatronics and Dynamic Systems, American Society for Engineering Education conference, Los Angeles, April 4-5, 2019, Paper ID #27850.

[18]M. Nielsen, I. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, New York, USA, 2011. Farbod Khoshnoud, Ph

Farbod Khoshnoud, PhD, CEng, PGCE, HEA Fellow, is a faculty member in the college of engineering at California State Polytechnic University, Pomona, and a visiting associate in the Center for Autonomous Systems and Technologies, in the department of Aerospace Engineering at California Institute of Technology. His current research areas include Self-powered and Bio-inspired Dynamic Systems; Quantum Multibody Dynamics, Robotics, Controls and Autonomy, by experimental Quantum Entanglement, and Quantum Cryptography; and theoretical Quantum Control techniques. He was a research affiliate at NASA’s Jet Propulsion Laboratory, Caltech in 2019, an Associate Professor of Mechanical Engineering at California State University, 2016-18, a visiting Associate Professor in the Department of Mechanical Engineering at the University of British Columbia (UBC) in 2017, a Lecturer in the Department of Mechanical Engineering at Brunel University London, 2014-16, a senior lecturer and lecturer at the University of Hertfordshire, 2011-14, a visiting scientist and postdoctoral researcher in the Department of Mechanical Engineering at UBC, 2007-11, a visiting researcher at California Institute of Technology, 2009-11, a Postdoctoral Research Fellow in the Department of Civil Engineering at UBC, 2005-2007. He received his Ph.D. from Brunel University in 2005. He is an associate editor of the Journal of Mechatronic Systems and Control.

Prof. Lucas Lamata is an Associate Professor (Profesor Titular de Universidad) of Theoretical Physics at the Departamento de Física Atómica, Molecular y Nuclear, Facultad de Física, Universidad de Sevilla, Spain. His research up to now has been focused on quantum optics and quantum information, including pioneering proposals for quantum simulations of relativistic quantum mechanics, fermionic systems, and spin models, with trapped ions and superconducting circuits. He also analyzes the possibility of combining artificial intelligence and machine learning protocols with quantum devices. Before working in Sevilla, HeI was a Staff Researcher (Investigador Doctor Permanente) at the University of the Basque Country, Bilbao, Spain (UPV/EHU), leading the Quantum Artificial Intelligence Team, a research group inside the QUTIS group of Prof. Enrique Solano at UPV/EHU. Before that, he was a Humboldt Fellow and a Max Planck postdoctoral fellow for 3 and a half years at the Max Planck Institute for Quantum Optics in Garching, Germany, working in Prof. Ignacio Cirac Group. Previously, he carried out his PhD at CSIC, Madrid, and Universidad Autónoma de Madrid (UAM), with an FPU predoctoral fellowship, supervised by Prof. Juan León. He has more than 100 articles, among published and submitted, in international refereed journals, including: 1 Nature, 1 Reviews of Modern Physics, 1 Advances in Physics: X, 3 Nature Communications, 2 Physical Review X, and 19 Physical Review Letters, two of them Editor's Suggestion. His h-index according to Google Scholar is of 35, with more than 4400 citations.

Clarence W. de Silva has been a Professor of Mechanical Engineering at the University of British Columbia, Vancouver, Canada since 1988. He received Ph.D. degrees from Massachusetts Institute of Technology and University of Cambridge, U.K., honorary D.Eng. degree from University of Waterloo, Canada, and the higher doctorate (ScD) from University of Cambridge. He is a Fellow of: IEEE, ASME, Canadian Academy of Engineering, and Royal Society of Canada. Also, he has been a Senior Canada Research Chair, NSERC-BC Packers Chair in Industrial Automation, Mobil Endowed Chair, Lilly Fellow, Senior Fulbright Fellow, Killam fellow, Erskine Fellow, Professorial Fellow, Faculty Fellow, Distinguished Visiting Fellow of Royal Academy of Engineering, UK, and a Peter Wall Scholar. He has authored 25 books and over 550 papers, approximately half of which are in journals. His recent books published by Taylor & Francis/CRC are: Modeling of Dynamic Systems—with Engineering Applications (2018); Sensor Systems (2017); Senors and Actuators— Engineering System Instrumentation, 2nd edition (2016); Mechanics of Materials (2014); Mechatronics—A Foundation Course (2010); Modeling and Control of Engineering Systems (2009); VIBRATION—Fundamentals and Practice, 2nd Ed. (2007); by Addison Wesley: Soft Computing and Intelligent Systems Design—Theory, Tools, and Applications (with Karray, 2004), and by Springer: Force and Position Control of Mechatronic Systems—Design and Applications in Medical Devices (with Lee, Liang and Tan, 2020).

Dr. Quadrelli is a Principal Member of the Technical Staff, and the supervisor of the Robotics Modeling and Simulation Group at JPL. He has a degree in Mechanical Engineering from Padova (Italy), an M.S. in Aeronautics and Astronautics from MIT, and a PhD in Aerospace Engineering from Georgia Tech. After joining NASA JPL in 1997 he has contributed to a number of flight projects including the Cassini-Huygens Probe, Deep Space One, the Mars Aerobot Test Program, the Mars Exploration Rovers, the Space Interferometry Mission, the Autonomous Rendezvous Experiment, and the Mars Science Laboratory, among others. He has been the Attitude Control lead of the Jupiter Icy Moons Orbiter Project, and the Integrated Modeling Task Manager for the Laser Interferometer Space Antenna. He has led or participated in several independent research and development projects in the areas of computational micromechanics, dynamics and control of tethered space systems, formation flying, inflatable apertures, hypersonic entry, precision landing, flexible multibody dynamics, guidance, navigation and control of spacecraft swarms, terra-mechanics, and precision pointing for optical systems. He is an Associate Fellow of the American Institute of Aeronautics and Astronautics, a NASA Institute of Advanced Concepts Fellow, and a Caltech/Keck Institute for Space Studies Fellow.

Cal Poly Pomona Arxiv

Wasp is a modern, declarative language that enables developers to rapidly build full-stack web applications. By abstracting the complexities of setting up both the server and the client, Wasp lets you focus on your application’s logic and design. In this article, we’ll walk through creating a simple full-stack app that includes a server API endpoint and a front-end that fetches and displays data from that endpoint.

Application Overview​

Our example application, MyFullStackApp, demonstrates how to:

• Define the overall app configuration.
• Set up a routing structure for navigation.
• Build a React-based front-end component.
• Create a server endpoint that responds with a greeting message.

The complete code example is shown below.

Code Example​

app MyFullStackApp {
  title: "My Full-Stack Wasp App"
  description: "A full-stack application example built with Wasp that integrates server and front-end components."
}

route HomeRoute {
  path: "/"
  component: HomePage
}

page HomePage {
  component: HomePageComponent
}

component HomePageComponent {
  <div>
    <h1>Welcome to My Full-Stack Wasp App!</h1>
    <p>This example demonstrates how to connect your front-end with a server API.</p>
    <GreetingComponent/>
  </div>
}

component GreetingComponent {
  <script>
    import React, { useEffect, useState } from 'react';

    function GreetingComponent() {
      const [greeting, setGreeting] = useState("");

      useEffect(() => {
        fetch("/api/greeting")
          .then(response => response.json())
          .then(data => setGreeting(data.greeting))
          .catch(error => console.error("Error fetching greeting:", error));
      }, []);

      return (
        <div>
          <p>{greeting ? greeting : "Loading greeting..."}</p>
        </div>
      );
    }

    export default GreetingComponent;
  </script>
}

server getGreeting {
  handler: function(req, res) {
    // Respond with a greeting message in JSON format
    res.json({ greeting: "Hello from the server!" });
  },
  method: "GET",
  path: "/api/greeting"
}

Detailed Explanation​

1. Application Setup​

• App Definition:

  The app block defines the general configuration for the application, such as its title and description. This acts as a central declaration point for your project.

• Routing:

  The route HomeRoute block maps the root path ("/") to the HomePage page. This structure makes it easy to manage navigation within the app.

2. Front-End Components​

• Page and Component Structure:

  The HomePage page is linked to the HomePageComponent, which composes the visible UI elements. Within this component, a header and a brief description are provided, along with the inclusion of the GreetingComponent.

• GreetingComponent:

  This is a React component embedded within a Wasp component. The component uses React’s hooks:

  • useState: Initializes the greeting state variable.
  • useEffect: Performs a fetch request to the server endpoint /api/greeting when the component mounts.

The fetched greeting is then displayed on the page. Error handling is also included to log any issues during the fetch operation.

3. Server-Side Code​

• Server Endpoint:

  The server getGreeting block defines an API endpoint:

  • handler: A function that sends a JSON response with a greeting message.

  • method: The HTTP method (GET) used to access this endpoint.

  • path: The URL path (/api/greeting) where the server listens for requests.

This server code demonstrates a typical pattern of exposing backend functionality via a RESTful API, which the front-end can consume.

4. Integration of Server and Front-End​

• Data Flow:

  When a user visits the homepage, the HomePageComponent renders and includes the GreetingComponent. On mounting, the GreetingComponent makes a GET request to the /api/greeting endpoint. The server responds with a JSON payload containing the greeting, which is then rendered in the UI. This seamless integration between server and client is one of Wasp’s strengths.

• Declarative Structure:

  Wasp’s declarative syntax helps keep the code organized. Developers can easily see how the app is structured, which routes lead to which pages, and how components are interconnected with server actions.

How to Install, Run, and Deploy a Wasp Application

1. Prerequisites​

Before you begin, make sure you have the following installed on your system:

• Node.js and npm:

Verify the installation with these commands:

node -v
npm -v

2. Installing Wasp CLI​

Method 1: Using curl​

curl -L https://get.wasp-lang.dev | sh

Method 2: Using npm​

npm install -g wasp-lang

3. Creating a New Project​

Once the Wasp CLI is installed, you can create a new project by running:

Create a New Project:

wasp new my-fullstack-app

Navigate to the Project Directory:

cd my-fullstack-app

4. Running the Application in Development Mode​

wasp start

5. Building the Production Version​

When you are ready to deploy your app for end users, you need to create a production build:

wasp build

6. Deploying the Application​

Deploying with Docker

FROM node:14
WORKDIR /app
COPY . .
RUN npm install
RUN wasp build
CMD ["npm", "start"]

Build the Docker Image:

docker build -t my-fullstack-app .

Run the Docker Container:

docker run -p 3000:3000 my-fullstack-app

In today’s fast-paced digital world, automation is no longer a luxury—it’s a necessity. n8n.io is an open-source workflow automation tool that enables you to automate repetitive tasks, integrate various services, and streamline your operations with minimal coding. This guide will walk you through everything you need to know to get started with n8n, from understanding its benefits to launching and configuring your instance.

Fair-code workflow automation platform with native AI capabilities.
Combine visual building with
custom code, self-host or cloud, 400+ integrations.

What is n8n?​

n8n is a powerful, extendable workflow automation tool that allows users to create complex integrations between different applications without being constrained by proprietary platforms. It offers a visual interface where you can design workflows by connecting nodes representing various actions or triggers. Its open-source nature means you have full control over your data and can self-host your solution, making it ideal for businesses with specific security or compliance requirements.

Why Choose n8n?​

• Flexibility and Customization​

Open Source:​

With n8n, you get complete access to the source code, allowing you to customize workflows and integrate any service, regardless of whether it’s officially supported.

Self-Hosting:​

Running n8n on your own infrastructure ensures that you control your data and comply with internal security policies.

Extensibility:​

n8n’s modular architecture means you can easily extend its functionality by adding custom nodes or integrating new APIs.

• Cost Efficiency​

Free and Community-Driven:​

n8n is free to use, and its active community continuously contributes plugins, integrations, and improvements.

No Vendor Lock-In:​

Unlike many cloud-based solutions, n8n allows you to avoid being tied to a single vendor, giving you the freedom to scale and modify your workflows as needed.

• Ease of Use​

Visual Workflow Designer:​

Its intuitive drag-and-drop interface simplifies the process of designing and managing automation flows.

Rich Ecosystem:​

n8n supports a wide range of integrations, from popular cloud services to niche applications, reducing the need for custom API work.

Prerequisites for Launching n8n​

Before you dive into the setup, ensure you have the following:

A Server or Local Environment: n8n can run on your local machine for testing or on a production server for live workflows. Docker (Recommended): For a streamlined and reproducible setup, using Docker is highly recommended. Node.js and npm: If you prefer a manual installation, ensure that you have Node.js (version 14 or higher) and npm installed. Basic Command Line Knowledge: Familiarity with terminal commands will help you navigate the installation and configuration process. SSL Certificate (for Production): If you plan to expose n8n to the internet, using an SSL certificate is crucial for securing communications.

Quick Start​

Try n8n instantly with npx (requires Node.js):

npx n8n

Or deploy with Docker:

docker volume create n8n_data
docker run -it --rm --name n8n -p 5678:5678 -v n8n_data:/home/node/.n8n docker.n8n.io/n8nio/n8n

Resources

📚 Documentation

🔧 400+ Integrations

💡 Example Workflows

🤖 AI & LangChain Guide

👥 Community Forum

📖 Community Tutorials

When working with GitHub Actions, it’s common to generate a multitude of artifacts during builds, tests, and deployments. Over time, these artifacts can accumulate, taking up valuable space and making repository management more challenging. In many cases, you might find yourself needing to clean up these artifacts—whether to free up storage or simply to keep your project tidy.

In this article, we’ll discuss the problem of excess artifacts and provide a simple code example that can help you clean them up from outside GitHub.

The Problem: Too Many Artifacts​

GitHub Actions provides a convenient way to build, test, and deploy your projects. However, every time an action runs, it can produce artifacts—files and reports that may be needed for debugging or archiving. While these artifacts can be invaluable for troubleshooting, they can also accumulate rapidly, especially in projects with frequent builds or extensive test suites.

Some common issues include:

- Storage Overhead:​

Excess artifacts can occupy significant space, leading to potential storage limits or unnecessary clutter.

- Organization:​

A large number of artifacts can make it hard to locate important information quickly.

- Performance:​

Managing a cluttered repository might indirectly affect build performance or other maintenance tasks.

Why Clean Up Artifacts?​

Cleaning up artifacts is not just about saving space; it also helps in maintaining a clean, organized repository. Regular cleanup routines can:

- Improve Readability:​

Removing outdated or unnecessary files makes it easier for you and your team to navigate your repository.

- Ensure Compliance:​

Some projects may have policies or storage limits, requiring periodic purging of unused artifacts.

- Enhance Performance:​

A cleaner environment might lead to faster build times and fewer errors related to storage limits.

While GitHub itself offers some artifact retention policies, there are scenarios where you might need more granular control, especially when cleaning up from outside GitHub using scripts or external tools.

Cleaning Up Artifacts from Outside GitHub​

Using GitHub’s REST API, you can programmatically list and delete artifacts. This method is particularly useful if you want to integrate cleanup into your CI/CD pipeline, schedule regular maintenance, or manage artifacts from an external system.

Below is a simple Python script that demonstrates how to list and delete artifacts from a GitHub repository. This code uses the requests library to interact with the GitHub API.

Sample Code: Python Script for Artifact Cleanup​

import requests

# Replace with your GitHub personal access token
GITHUB_TOKEN = 'your_github_token'
# Replace with your repository details
OWNER = 'your_repo_owner'
REPO = 'your_repo_name'

# Set up the headers for authentication
headers = {
    "Authorization": f"token {GITHUB_TOKEN}",
    "Accept": "application/vnd.github.v3+json"
}

def list_artifacts():
    """List all artifacts in the repository."""
    url = f"https://api.github.com/repos/{OWNER}/{REPO}/actions/artifacts"
    response = requests.get(url, headers=headers)

    if response.status_code != 200:
        print(f"Failed to fetch artifacts: {response.status_code} - {response.text}")
        return []

    data = response.json()
    return data.get('artifacts', [])

def delete_artifact(artifact_id, artifact_name):
    """Delete an artifact by its ID."""
    delete_url = f"https://api.github.com/repos/{OWNER}/{REPO}/actions/artifacts/{artifact_id}"
    response = requests.delete(delete_url, headers=headers)

    if response.status_code == 204:
        print(f"Deleted artifact '{artifact_name}' (ID: {artifact_id}) successfully.")
    else:
        print(f"Failed to delete artifact '{artifact_name}' (ID: {artifact_id}): {response.status_code} - {response.text}")

def cleanup_artifacts():
    """Fetch and delete all artifacts."""
    artifacts = list_artifacts()

    if not artifacts:
        print("No artifacts found.")
        return

    print(f"Found {len(artifacts)} artifacts. Starting cleanup...")
    for artifact in artifacts:
        artifact_id = artifact['id']
        artifact_name = artifact['name']
        delete_artifact(artifact_id, artifact_name)

if __name__ == "__main__":
    cleanup_artifacts()

How to Use the Script​

1. Install Dependencies: Ensure you have Python installed, and install the requests library if you haven’t already:

pip install requests

2. Configure the Script: Replace the placeholders your_github_token, your_repo_owner, and your_repo_name with your actual GitHub personal access token and repository details.

3. Run the Script: Execute the script from your command line:

python cleanup_artifacts.py

The script will list all artifacts and attempt to delete each one. You can modify the script to include filters (such as deleting only artifacts older than a certain date) based on your requirements.

Final Thoughts​

Managing artifacts is a crucial aspect of maintaining a clean and efficient CI/CD workflow. While GitHub offers basic artifact management features, using external scripts like the one above provides you with greater control and flexibility. You can easily schedule this script using a cron job or integrate it into your own maintenance pipeline to ensure that your repository stays free of clutter.

Regular cleanup not only saves storage space but also helps in keeping your repository organized and performant. Feel free to customize the sample code to better fit your specific needs, such as filtering artifacts by creation date, size, or naming conventions.

Happy coding and maintain a tidy repository!

Introduction​

Ollama is a powerful tool for running large language models efficiently on local hardware. When combined with DeepSpeed, a deep learning optimization library, it enables even more efficient execution, particularly for fine-tuning and inference. In this guide, we will walk through the setup process for both Ollama and DeepSpeed on a Linux system.

Prerequisites​

Before proceeding, ensure that your system meets the following requirements:

• A Linux-based operating system (Ubuntu 20.04 or later recommended)

• A modern NVIDIA GPU with CUDA support

• Python 3.8 or later

• Pip and Virtualenv installed

• Sufficient storage and RAM for model execution

Step 1: Installing Ollama​

Ollama provides an easy-to-use interface for managing large language models. To install it on Linux, follow these steps:

1. Open a terminal and update your system:​

sudo apt update && sudo apt upgrade -y

2. Download and install Ollama:​

curl -fsSL https://ollama.ai/install.sh | sh

3. Verify the installation:​

ollama --version

If the installation was successful, you should see the version number displayed.

Step 2: Setting Up DeepSpeed​

DeepSpeed optimizes deep learning models for better performance and scalability. To install and configure it:

1. Create and activate a Python virtual environment:​

python3 -m venv deepspeed_env
source deepspeed_env/bin/activate

2. Install DeepSpeed and required dependencies:​

pip install deepspeed torch transformers

3. Verify the installation:​

deepspeed --version

Step 3: Running a Model with Ollama and DeepSpeed​

Now that we have both tools installed, we can load a model and test it.

1. Pull a model with Ollama:​

ollama pull mistral

This downloads the Mistral model, which we will use for testing.

2. Run inference with Ollama:​

ollama run mistral "Hello, how are you?"

If successful, the model should generate a response.

3. Use DeepSpeed to optimize inference (example using a Hugging Face model):​

from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
import deepspeed

model_name = "meta-llama/Llama-2-7b"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name, torch_dtype=torch.float16)

ds_model = deepspeed.init_inference(model, dtype=torch.float16, replace_with_kernel_inject=True)

prompt = "What is DeepSpeed?"
inputs = tokenizer(prompt, return_tensors="pt").to("cuda")
outputs = ds_model.generate(**inputs)
print(tokenizer.decode(outputs[0]))

Example : Deepseek-r1 1.5b​

Conclusion​

By installing Ollama and DeepSpeed on Linux, you can efficiently run and optimize large language models. This setup enables users to leverage local hardware for AI model execution, reducing dependency on cloud services. If further fine-tuning or model adaptation is required, both tools provide advanced functionalities to enhance performance.

Filecoin FVM Localnet is a Docker-based solution that simplifies the process of deploying a local Filecoin network for smart contract development. This setup supports testing of Filecoin Virtual Machine (FVM) smart contracts and features such as replication between storage providers (SPs).

System Requirements​

To run Filecoin FVM Localnet, you’ll need:

• Processor Architecture: ARM64 (e.g., MacBook M1/M2) or AMD64 (e.g., x86 Linux, Windows, macOS).

• Docker: Ensure Docker is installed on your system.

Installation​

Step 1: Clone the Repository​

Run the following command to clone the Filecoin FVM Localnet repository:

git clone https://github.com/filecoin-project/filecoin-fvm-localnet.git

Step 2: Navigate to the Repository​

cd filecoin-fvm-localnet

Step 3: Configure the Environment​

To use the default configuration with 2k sectors:

cp .env.example .env

To configure an 8MiB sector network, edit the .env file to enable the relevant settings.

Step 4: Start the Localnet​

To run a single miner instance:

docker compose up

To run two miners with replication capabilities:

docker compose --profile replication up

Stop the network using Ctrl+C.

Step 5: Access the Boost UI​

Once the localnet is running, you can access the Boost UI:

• Primary Boost instance: http://localhost:8080

• Secondary Boost instance (if replication is enabled): http://localhost:8081

Setting Up Metamask​

Configuring Metamask​

1. Open Metamask and click on the network dropdown at the top.

2. Click Add a network manually and enter the following details:

• • Network Name: Filecoin localnet
• • RPC URL: http://127.0.0.1:1234/rpc/v1
• • Chain ID: 31415926
• • Currency Symbol: tFIL

Funding a Wallet​

1. Retrieve the t4 address for your wallet using the following command :

docker compose exec lotus lotus evm stat [wallet]

2. Send test funds (tFIL) to your wallet using:

docker compose exec lotus lotus send <t4_address> 1000

Funds will appear in Metamask within approximately 45 seconds.

Usage Notes​

Sector Sizes and Block Time​

• Default sector size: 2KiB (maximum storage deal size).

• Optional: Configure for 8MiB sectors by editing .env and restarting the localnet.

• Block time: 15 seconds (half the time of the Filecoin mainnet).

Resetting the Localnet​

If the network takes a long time to sync, delete the data/ directory and restart the localnet to reset the state.

Common Commands for Filecoin FVM Localnet​

Packing Files for Deals​

1. Pack files into CAR format:

ipfs-car pack [file] --output [filename].car

2. Generate CommP for the packed CAR file:

boostx commp [file.car]

Creating a Storage Deal​

boost deal --verified=false \
           --provider=[minerId] \
           --http-url=[file-address-on-server] \
           --commp=<commp_value> \
           --car-size=<car_file_size> \
           --piece-size=<piece_size> \
           --payload-cid=<payload_cid> \
           --storage-price=[estimate-number] \
           --duration=[time]

Checking Deal Status​

Retrieve the status of a deal:

boost deal-status --provider=<provider_id> --deal-uuid=<deal_uuid>

Retrieving Stored Data​

To retrieve stored data:

boost retrieve --provider=<provider_id> --output=/path/to/output/file.car <payload_cid>

Module Lattice Based Key Encapsulation Mechanism Standard​

An In-Depth Exploration of the ML-KEM Standard​

The source provided is the official FIPS 203 document specifying the Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) standard. It aims to provide a complete guide for implementing ML-KEM, a cryptographic algorithm designed to resist attacks from quantum computers. This response will explore the key concepts of the ML-KEM standard, the rationale behind its design, and important implementation considerations.

The Quantum Threat and the Rise of Post-Quantum Cryptography​

Before examining ML-KEM itself, it is crucial to understand the context that led to its creation. Modern cryptography relies heavily on public-key cryptosystems, which are essential for tasks like secure key exchange and digital signatures. These cryptosystems are built upon mathematical problems that are computationally hard for classical computers to solve.

However, the advent of quantum computing presents a significant threat to these systems. Quantum computers leverage the principles of quantum mechanics to perform computations in a fundamentally different way than classical computers. This allows them to efficiently solve certain problems that are intractable for classical computers, including the factoring of large numbers and the discrete logarithm problem. These problems form the foundation of many widely used public-key cryptosystems, such as RSA and elliptic curve cryptography.

If large-scale, fault-tolerant quantum computers become a reality, they could break the security of these cryptosystems, rendering sensitive data vulnerable to attacks. To address this emerging threat, the field of post-quantum cryptography (PQC) has emerged. The goal of PQC is to develop cryptographic algorithms that are resistant to attacks from both classical and quantum computers.

Recognizing the urgency of this issue, NIST initiated the PQC Standardization process to evaluate and standardize new quantum-resistant public-key cryptographic algorithms. This process involved multiple rounds of public scrutiny, analysis, and evaluation of submitted candidate algorithms. ML-KEM emerged as one of the algorithms selected for standardization.

Key-Encapsulation Mechanisms: The Heart of Secure Key Exchange​

ML-KEM is a specific type of cryptographic algorithm known as a key-encapsulation mechanism (KEM). KEMs are designed for the secure exchange of cryptographic keys between two parties over a public channel.

Understanding the Role of KEMs​

In a typical key exchange scenario, two parties, often referred to as Alice and Bob, want to communicate securely. To do so, they need to establish a shared secret key. A KEM enables them to achieve this goal even if their communication channel is insecure and potentially eavesdropped upon. Here's a simplified overview of how a KEM works:

• Key Generation: Alice uses a KEM's key generation algorithm to generate two keys: a public encapsulation key (analogous to a public key) and a private decapsulation key (analogous to a private key).
• Encapsulation: Bob, upon receiving Alice's encapsulation key, uses the KEM's encapsulation algorithm to generate a shared secret key and an associated ciphertext.
• Transmission: Bob sends the ciphertext to Alice.
• Decapsulation: Alice, using her decapsulation key and the received ciphertext, runs the KEM's decapsulation algorithm to recover the shared secret key.

Key Properties of a Secure KEM:​

• Correctness: A KEM should ensure that if both parties follow the protocol correctly, they will derive the same shared secret key.
• Security: A secure KEM must prevent an adversary from learning anything about the shared secret key even if they intercept the ciphertext and have access to -the encapsulation key.

ML-KEM: A Module-Lattice-Based Approach to Security​

ML-KEM is based on a mathematical problem called the Module Learning With Errors (MLWE) problem. This problem is believed to be computationally hard, even for quantum computers. It leverages the structure of mathematical objects called modules, which are essentially generalizations of vector spaces. The MLWE problem involves finding a specific solution within a module, given a set of noisy linear equations. Let's break down the core concepts involved in the MLWE problem:

• Modules: A module is an algebraic structure that consists of:

  • A set of elements.
  • An operation for adding elements (similar to vector addition).
  • An operation for multiplying elements by scalars (similar to scalar multiplication in vector spaces).

• Lattices: Lattices are a specific type of module where the elements are represented by points in a grid-like structure. They play a crucial role in post-quantum cryptography due to their inherent geometric properties and the difficulty of certain computational problems related to them.

• Learning With Errors (LWE) Problem: The LWE problem involves finding a secret vector given a set of noisy linear equations. The noise is intentionally added to make the problem difficult to solve.

• Module Learning With Errors (MLWE) Problem: The MLWE problem extends the LWE problem to work with modules instead of vectors. This adds another layer of complexity to the problem, making it even more challenging for attackers to solve.

• The security of ML-KEM is rooted in the assumption that solving the MLWE problem is computationally hard for both classical and quantum computers.

Building ML-KEM from K-PKE: A Two-Step Construction​

The construction of ML-KEM proceeds in two steps:

• Creating a Public-Key Encryption Scheme: First, the principles of the MLWE problem are used to construct a public-key encryption (PKE) scheme called K-PKE. This scheme allows for encryption and decryption of messages using a public and private key pair. However, K-PKE alone does not provide the desired level of security for key exchange.

• Applying the Fujisaki-Okamoto (FO) Transform: To enhance the security of K-PKE and transform it into a robust KEM, the Fujisaki-Okamoto (FO) transform is applied. This transform is a well-established technique in cryptography that strengthens the security of a PKE scheme. It achieves this by:

• Derandomizing the encryption process: This removes potential vulnerabilities arising from the use of predictable or weak randomness.

• Adding checks and safeguards: The FO transform incorporates checks to ensure that the ciphertext is well-formed and has not been tampered with.

The resulting KEM, ML-KEM, is believed to satisfy a strong security notion called IND-CCA2 security. This security level ensures that the KEM remains secure even against sophisticated attacks, such as chosen-ciphertext attacks.

Enhancing Efficiency with the Number-Theoretic Transform​

ML-KEM employs the number-theoretic transform (NTT) to optimize the performance of its operations. The NTT is a mathematical tool that enables efficient multiplication of polynomials. Polynomials play a key role in ML-KEM's calculations, and the NTT significantly speeds up these calculations. Understanding the NTT's Role:

• Fast Polynomial Multiplication: Polynomial multiplication can be a computationally expensive operation. The NTT allows for faster multiplication by transforming polynomials into a different representation where multiplication is more efficient.

• Transforming Between Representations: The NTT and its inverse transform can be used to convert between the standard representation of a polynomial and its NTT representation.

Illustrative Example:​

Consider two polynomials, f(x) and g(x), that need to be multiplied.

• Forward NTT: The NTT is applied to f(x) and g(x), resulting in their NTT representations, F and G.

• Efficient Multiplication: F and G are multiplied in the NTT domain. This multiplication is faster in the NTT domain than in the standard polynomial representation.

• Inverse NTT: The inverse NTT is applied to the product of F and G to obtain the product of f(x) and g(x) in the standard polynomial representation. This process of using the NTT for polynomial multiplication is considerably more efficient than directly multiplying f(x) and g(x). This efficiency gain is crucial for the performance of ML-KEM.

Parameter Sets: Balancing Security and Performance​

ML-KEM offers three different parameter sets, each providing a different trade-off between security strength and performance:

• ML-KEM-512 (Security Category 1): This parameter set offers a base level of security and the fastest performance. It is suitable for applications where performance is paramount and a moderate level of security is sufficient.

• ML-KEM-768 (Security Category 3): This set provides enhanced security compared to ML-KEM-512, but it comes at the cost of slightly slower performance. It strikes a balance between security and performance and is suitable for a wide range of applications.

• ML-KEM-1024 (Security Category 5): This parameter set provides the highest level of security but has the slowest performance among the three options. It is ideal for situations where maximum security is a top priority, even at the expense of some performance overhead.

The selection of the appropriate parameter set depends on the specific security requirements of the application and the available computational resources. Algorithms of ML-KEM: A Detailed Look

ML-KEM's functionality is implemented through three main algorithms:​

• ML-KEM.KeyGen (Algorithm 19 in the Sources):

• This algorithm generates an encapsulation key and a corresponding decapsulation key.

• The encapsulation key is made public, while the decapsulation key must be kept secret.

• The generation process involves using a random bit generator (RBG) to create random seeds. These seeds are then used to generate the keys using various mathematical operations, including the NTT.

• The sources recommend storing the seed generated during this process, as it can be used to regenerate the keys later, providing assurance of private key possession.

• ML-KEM.Encaps (Algorithm 20 in the Sources):

• This algorithm uses the encapsulation key (received from the other party) to create a shared secret key and a ciphertext.

• The process begins with generating a random value, m.

• The shared secret key, K, and a random value, r (used for encryption), are derived from m and the encapsulation key using hash functions.

• The K-PKE encryption scheme is used to encrypt m using the encapsulation key and the randomness r, resulting in the ciphertext c.

• The algorithm outputs the shared secret key K and the ciphertext c.

• ML-KEM.Decaps (Algorithm 21 in the Sources):

• This algorithm utilizes the decapsulation key (the party's own private key) and a received ciphertext to derive the shared secret key.

• The decapsulation key contains several components: the decryption key of the K-PKE scheme, a hash value of the encapsulation key, and a random value z (used for implicit rejection in case of errors).

• The K-PKE decryption algorithm is used to decrypt the ciphertext c and obtain a plaintext value m'.

• To ensure correctness and prevent certain types of attacks, the algorithm re-encrypts m' using the derived randomness and compares the resulting ciphertext with the received ciphertext c.

• If the ciphertexts match: The algorithm outputs the derived shared secret key, K'.

• If the ciphertexts do not match: This indicates a potential error or attack. In this case, the algorithm performs an "implicit rejection" by deriving a different shared secret key based on the random value z and the ciphertext. This prevents the attacker from learning anything about the actual shared secret key.

Crucial Implementation Considerations​

The sources emphasize the importance of adhering to specific implementation details to ensure the security and correctness of ML-KEM. Key considerations include:

• Randomness Generation: The algorithms of ML-KEM heavily depend on randomness for generating keys, encryption randomness, and other operations. This randomness must be generated using an approved random bit generator (RBG) that meets specific security strength requirements. Using a weak or predictable RBG would compromise the security of the entire scheme.

• Input Checking: Input checking is critical to prevent potential vulnerabilities that can arise from processing malformed or invalid inputs. ML-KEM mandates specific input checks for both encapsulation and decapsulation. These checks ensure that:

• Encapsulation Key Check: The encapsulation key is a valid byte array with the correct length and encodes valid integers within the expected range.

• Decapsulation Key Check: The decapsulation key has the correct length and contains internally consistent data.

• Ciphertext Check: The ciphertext has the correct length for the chosen parameter set.

• Prohibition of K-PKE as a Standalone Scheme: K-PKE, the public-key encryption scheme used as a building block for ML-KEM, is not sufficiently secure to be used as a standalone cryptographic scheme. It should only be employed within the context of the ML-KEM construction, where the FO transform and other security measures provide the necessary level of protection.

• Controlled Access to Internal Functions: The ML-KEM scheme makes use of several internal functions, such as ML-KEM.KeyGen_internal, ML-KEM.Encaps_internal, and ML-KEM.Decaps_internal. These functions are designed for specific internal operations and should not be exposed directly to applications, except for testing purposes. The cryptographic module should handle the generation of random values and manage access to these internal functions to prevent potential misuse.

• Proper Handling of Decapsulation Failures: While ML-KEM is designed to minimize decapsulation failures (cases where the decapsulated key does not match the encapsulated key), they can occur due to various factors, including transmission errors or intentional modifications of the ciphertext. The "implicit rejection" mechanism in ML-KEM.Decaps is essential for handling such failures securely. It ensures that even if an attacker intentionally causes a decapsulation failure, they cannot gain any information about the legitimate shared secret key.

• Approved Usage of the Shared Secret Key: The shared secret key produced by ML-KEM should be used in accordance with established cryptographic guidelines. It can be directly used as a symmetric key or, if needed, further processed using an approved key derivation function (KDF) to create additional keys.

Differences from CRYSTALS-KYBER​

While ML-KEM is based on the CRYSTALS-KYBER algorithm, there are some key differences that impact the input-output behavior of the algorithms:

Removal of Pre-Hashing in Encapsulation: In the third-round specification of CRYSTALS-KYBER, the initial randomness used in the ML-KEM.Encaps algorithm was hashed before use. This was intended as a safeguard against the potential use of flawed randomness. However, as ML-KEM mandates the use of approved RBGs, this pre-hashing step is deemed unnecessary and has been removed in the ML-KEM standard.

Inclusion of Explicit Input Checks: ML-KEM explicitly incorporates input checking steps in its algorithms to ensure the validity of the input data. These checks are designed to detect and prevent issues arising from malformed or invalid inputs. This is a security enhancement that was not explicitly included in the original CRYSTALS-KYBER specification.

Domain Separation in K-PKE.KeyGen: Based on comments received during the public draft phase of FIPS 203, domain separation was added to the K-PKE.KeyGen algorithm to prevent the misuse of keys generated for one security level at a different security level. This ensures that keys are used consistently with their intended security level.

Index Correction in Matrix A: During the initial public draft phase, the indices of the matrix A in K-PKE.KeyGen and K-PKE.Encrypt were inadvertently swapped. This has been corrected in the final version of ML-KEM to align with the CRYSTALS-KYBER specification, ensuring consistency and proper functionality.

Concluding Remarks​

The ML-KEM standard marks a significant step towards securing digital communications in the age of quantum computing. It leverages the strength of lattice-based problems, believed to be resistant to quantum attacks, to provide a robust mechanism for secure key exchange.

The sources provide a comprehensive and detailed technical specification of ML-KEM, highlighting its algorithms, parameter sets, and critical implementation considerations. The differences between ML-KEM and its predecessor, CRYSTALS-KYBER, are outlined to facilitate a smooth transition for implementers.

The standard is primarily targeted towards technical audiences involved in implementing and deploying cryptographic systems. While it offers insights into the rationale and security considerations behind design choices, it assumes a good understanding of cryptographic concepts and mathematical principles.

Reference : https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.203.ipd.pdf

Trusted Execution Environment (TEE) with Rust and AWS​

Trusted Execution Environments (TEEs) are critical for modern applications where sensitive data needs to be processed securely. By isolating code execution from the rest of the system, TEEs provide a secure enclave where data and computations are shielded from unauthorized access, even in cases where the operating system is compromised. In this article, we will explore how to leverage TEEs using Rust—a system programming language known for its safety and performance—along with AWS services to build secure and efficient applications.

Overview of TEE​

Key Features of TEE​

• Isolation: Secure enclave segregates sensitive code and data from the rest of the system.

• Attestation: Remote parties can verify the integrity of the TEE before trusting it with sensitive data.

• Encryption: Data within the TEE is encrypted and inaccessible from outside.

Use Cases of TEE​

• Secure key management

• Processing confidential data, such as financial transactions

• Privacy-preserving machine learning

Why Use Rust for TEE?​

Rust is an excellent choice for working with TEEs due to its:

• Memory Safety: Rust prevents common vulnerabilities like buffer overflows.

• Concurrency Without Data Races: Rust’s ownership model ensures safe multithreading.

• Performance: Rust’s zero-cost abstractions deliver C-like performance.

Additionally, Rust has libraries and tools to interact with TEEs, such as Intel SGX SDKs and AMD SEV frameworks.

TEE on AWS​

AWS provides various services to integrate TEEs into your applications:

• AWS Nitro Enclaves: Isolate sensitive computations in secure enclaves on AWS EC2 instances.

• AWS Key Management Service (KMS): Manage encryption keys securely.

• AWS Lambda with AWS Enclaves: Enable serverless applications to process sensitive data securely.

Implementing a Secure TEE Application with Rust and AWS​

In this section, we will create a secure application using AWS Nitro Enclaves and Rust. Our application will:

1. Receive sensitive data.

2. Process the data securely in a Nitro Enclave.

3. Return the result to the client.

Prerequisites​

1. Rust Development Environment: Install Rust and set up your development environment using rustup.

2. AWS CLI and Nitro CLI: Install and configure these tools on your EC2 instance.

3. Nitro Enclaves-enabled EC2 Instance: Launch an EC2 instance with support for Nitro Enclaves.

Step 1: Setting Up the Nitro Enclave​

Configure Your EC2 Instance​

Ensure your EC2 instance is Nitro Enclaves-compatible and has enclave support enabled:

sudo nitro-cli-config -i sudo nitro-cli-config -m auto

Build the Enclave Image​

Create an enclave image file (eif) containing the application binary:

docker build -t enclave-app .
nitro-cli build-enclave --docker-uri enclave-app --output-file enclave.eif

Run the Enclave​

Launch the enclave using Nitro CLI:

nitro-cli run-enclave --eif-path enclave.eif --memory 2048 --cpu-count 2

Step 2: Developing the Rust Application​

Application Requirements​

The Rust application will:

• Listen for client requests.

• Process sensitive data securely within the enclave.

• Return encrypted responses.

Application Code​

Here’s the Rust code for the application:

main.rs:

use std::io::{Read, Write};
use std::net::{TcpListener, TcpStream};
use serde::{Deserialize, Serialize};
use aes_gcm::{Aes256Gcm, Key, Nonce}; // Encryption library
use aes_gcm::aead::{Aead, NewAead};

#[derive(Serialize, Deserialize)]
struct Request {
message: String,
}

#[derive(Serialize, Deserialize)]
struct Response {
encrypted_message: Vec<u8>,
}

fn handle_client(mut stream: TcpStream, key: &Key) {
let mut buffer = [0; 1024];
stream.read(&mut buffer).unwrap();

    let request: Request = serde_json::from_slice(&buffer).unwrap();
    println!("Received: {}", request.message);

    // Encrypt the message
    let cipher = Aes256Gcm::new(key);
    let nonce = Nonce::from_slice(b"unique nonce");
    let ciphertext = cipher.encrypt(nonce, request.message.as_bytes()).unwrap();

    let response = Response {
        encrypted_message: ciphertext,
    };

    let response_json = serde_json::to_vec(&response).unwrap();
    stream.write_all(&response_json).unwrap();

}

fn main() {
let listener = TcpListener::bind("0.0.0.0:8080").unwrap();
println!("Server listening on port 8080");

    // Generate a secure key for encryption
    let key = Key::from_slice(b"an example very very secret key.");

    for stream in listener.incoming() {
        match stream {
            Ok(stream) => {
                handle_client(stream, key);
            }
            Err(e) => {
                eprintln!("Error: {}", e);
            }
        }
    }

}

Key Points​

• Encryption: The application uses AES-256-GCM to encrypt data securely.

• Serialization: Rust’s serde library handles JSON serialization/deserialization.

Step 3: Integrating with AWS KMS​

Use AWS KMS to manage and provision encryption keys:

Example: Encrypting Data with KMS​

aws kms encrypt \
 --key-id alias/YourKMSKeyAlias \
 --plaintext fileb://plaintext-file \
 --output text \
 --query CiphertextBlob > encrypted-file

Decrypt the data inside the enclave using the AWS KMS API.

Step 4: Secure Communication​

Secure communication between the client and the enclave using TLS. You can use libraries like rustls or tokio for TLS support.

Example: Adding TLS to the Server​

use tokio_rustls::TlsAcceptor;
use tokio::net::TcpListener;

// Implement TLS listener with certificate and private key.

Testing the TEE Application​

• Unit Testing: Test individual Rust functions, especially encryption and decryption.

• Integration Testing: Verify communication between the client and the enclave.

• End-to-End Testing: Simulate real-world scenarios to ensure data is processed securely.

Conclusion​

Combining Rust’s safety features with AWS Nitro Enclaves allows developers to build highly secure applications that process sensitive data. By leveraging TEEs, you can achieve data isolation, integrity, and confidentiality even in hostile environments. With the provided example, you now have a foundation to build your own TEE-powered applications using Rust and AWS.